Contents

Estimating damping and depth parameters

Estimating damping and depth parameters

When interpolating gravity and magnetic data through the Equivalent Sources technique we need to choose values for some parameters, like the depth at which the sources will be located or the amount of damping that should be applied.

The choice of these hyperparameters can significantly affect the accuracy of the predictions. One way to make this choice could be a visual inspection of the predictions, but that could be tedious and non-objective. Instead, we could estimate these hyperparameters by evaluating the performance of the equivalent sources with different values for each hyperparameter through a cross validation.

See also

Evaluating the performance of EquivalentSources through cross validation is very similar to how we do it for any verde gridder. Refer to Verde’s Evaluating Performance and Model Selection for further details.

Cross-validating equivalent sources

Lets start by loading some sample gravity data:

import ensaio
import pandas as pd

fname = ensaio.fetch_bushveld_gravity(version=1)
data = pd.read_csv(fname)
data
longitude latitude height_sea_level_m height_geometric_m gravity_mgal gravity_disturbance_mgal gravity_bouguer_mgal
0 25.01500 -26.26334 1230.2 1257.474535 978681.38 25.081592 -113.259165
1 25.01932 -26.38713 1297.0 1324.574150 978669.02 24.538158 -122.662101
2 25.02499 -26.39667 1304.8 1332.401322 978669.28 26.526960 -121.339321
3 25.04500 -26.07668 1165.2 1192.107148 978681.08 17.954814 -113.817543
4 25.07668 -26.35001 1262.5 1289.971792 978665.19 12.700307 -130.460126
... ... ... ... ... ... ... ...
3872 31.51500 -23.86333 300.5 312.710241 978776.85 -4.783965 -39.543608
3873 31.52499 -23.30000 280.7 292.686630 978798.55 48.012766 16.602026
3874 31.54832 -23.19333 245.7 257.592670 978803.55 49.161771 22.456674
3875 31.57333 -23.84833 226.8 239.199065 978808.44 5.116904 -20.419870
3876 31.37500 -23.00000 285.6 297.165672 978734.77 5.186926 -25.922627

3877 rows × 7 columns

And project their coordinates using a Mercator projection:

import pyproj

projection = pyproj.Proj(proj="merc", lat_ts=data.latitude.values.mean())
easting, northing = projection(data.longitude.values, data.latitude.values)

coordinates = (easting, northing, data.height_geometric_m.values)

Lets fit the gravity disturbance using equivalent sources and a first guess for the depth and damping parameters.

import harmonica as hm

eqs_first_guess = hm.EquivalentSources(depth=1e3, damping=1)
eqs_first_guess.fit(coordinates, data.gravity_disturbance_mgal)

EquivalentSources(damping=1, depth=1000.0)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can use a cross-validation to evaluate how well these equivalent sources can accurately predict the values of the field on unobserved locations. We will use verde.cross_val_score and then we will compute the mean value of the score obtained after each cross validation.

import numpy as np
import verde as vd

score_first_guess = np.mean(
    vd.cross_val_score(
        eqs_first_guess,
        coordinates,
        data.gravity_disturbance_mgal,
    )
)
score_first_guess

0.8027851941632994

The resulting score corresponds to the R^2. It represents how well the equivalent sources can reproduce the variation of our data. As closer it gets to one, the better the quality of the predictions.

Estimating hyperparameters

We saw that we can evaluate the performance of some equivalent sources with some values for the depth and damping parameters through cross validation. Now, lets use it to estimate a set of hyperparameters that produce more accurate predictions. To do so we are going to apply a simple grid search over the depth, damping space, apply cross validation for each pair of values and keeping track of their score.

Lets start by defining some possible values of damping and depth to explore:

dampings = [0.01, 0.1, 1, 10,]
depths = [5e3, 10e3, 20e3, 50e3]

Note

The actual value of the damping is not significant as its order of magnitude. Exploring different powers of ten is a good place to start.

Then we can build a parameter_sets list where each element corresponds to each possible combination of the values of dampings and depths:

import itertools

parameter_sets = [
    dict(damping=combo[0], depth=combo[1])
    for combo in itertools.product(dampings, depths)
]
print("Number of combinations:", len(parameter_sets))
print("Combinations:", parameter_sets)

Number of combinations: 16
Combinations: [{'damping': 0.01, 'depth': 5000.0}, {'damping': 0.01, 'depth': 10000.0}, {'damping': 0.01, 'depth': 20000.0}, {'damping': 0.01, 'depth': 50000.0}, {'damping': 0.1, 'depth': 5000.0}, {'damping': 0.1, 'depth': 10000.0}, {'damping': 0.1, 'depth': 20000.0}, {'damping': 0.1, 'depth': 50000.0}, {'damping': 1, 'depth': 5000.0}, {'damping': 1, 'depth': 10000.0}, {'damping': 1, 'depth': 20000.0}, {'damping': 1, 'depth': 50000.0}, {'damping': 10, 'depth': 5000.0}, {'damping': 10, 'depth': 10000.0}, {'damping': 10, 'depth': 20000.0}, {'damping': 10, 'depth': 50000.0}]

And now we can actually ran one cross validation for each pair of parameters:

equivalent_sources = hm.EquivalentSources()

scores = []
for params in parameter_sets:
    equivalent_sources.set_params(**params)
    score = np.mean(
        vd.cross_val_score(
            equivalent_sources,
            coordinates,
            data.gravity_disturbance_mgal,
        )
    )
    scores.append(score)
scores

[0.9150928326896647,
 0.914224977302967,
 0.904390575238215,
 0.8822529497698314,
 0.9158120453861749,
 0.9179260104391922,
 0.9104311266643214,
 0.8751298775883054,
 0.9161113383638287,
 0.9197261730846152,
 0.9070261659773458,
 0.8619681875563364,
 0.9158209704190462,
 0.9172918887155357,
 0.894617327589027,
 0.8408182949960299]

Once every score has been computed, we can obtain the best score and the corresponding parameters that generate it:

best = np.argmax(scores)
print("Best score:", scores[best])
print("Score with defaults:", score_first_guess)
print("Best parameters:", parameter_sets[best])

Best score: 0.9197261730846152
Score with defaults: 0.8027851941632994
Best parameters: {'damping': 1, 'depth': 10000.0}

We have actually improved our score!

Finally, lets grid the gravity disturbance data using the equivalent sources of the first guess and the best ones obtained after cross validation.

Create some equivalent sources out of the best set of parameters:

eqs_best = hm.EquivalentSources(**parameter_sets[best]).fit(
    coordinates, data.gravity_disturbance_mgal
)

And grid the data using the two equivalent sources:

# Define grid coordinates
grid_coords = vd.grid_coordinates(
    region=vd.get_region(coordinates),
    spacing=2e3,
    extra_coords=2.5e3,
)

grid_first_guess = eqs_first_guess.grid(grid_coords)
grid = eqs_best.grid(grid_coords)

Lets plot it:

import matplotlib.pyplot as plt


maxabs = vd.maxabs(grid_first_guess.scalars, grid.scalars)

fig, (ax1, ax2) = plt.subplots(figsize=(12, 12), ncols=2, nrows=1, sharey=True)

cbar_kwargs = dict(orientation="horizontal", aspect=50, pad=0.05, label="mGal")
grid_first_guess.scalars.plot.pcolormesh(
    ax=ax1,
    vmin=-maxabs,
    vmax=maxabs,
    cmap="seismic",
    cbar_kwargs=cbar_kwargs,
)
grid.scalars.plot.pcolormesh(
    ax=ax2,
    vmin=-maxabs,
    vmax=maxabs,
    cmap="seismic",
    cbar_kwargs=cbar_kwargs,
)

ax1.set_title("Gravity disturbance with first guess")
ax2.set_title("Gravity disturbance with best params")
for ax in (ax1, ax2):
    ax.set_aspect("equal")
plt.show()
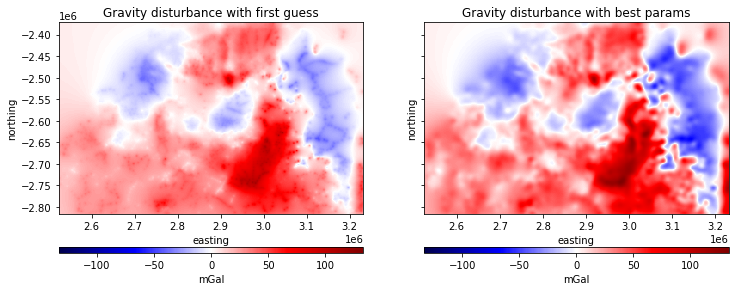
../../_images/eqs-parameters-estimation_10_0.png

The best parameters not only produce a better score, but they also generate a visible more accurate predictions. In the first plot the equivalent sources are so shallow that we can actually see the distribution of sources in the produced grid.

previous

Equivalent Sources

next

Block-averaged equivalent sources