Airy Isostatic Moho
Note
Click here to download the full example code
Airy Isostatic Moho¶
According to the Airy hypothesis of isostasy, topography above sea level is
supported by a thickening of the crust (a root) while oceanic basins are
supported by a thinning of the crust (an anti-root). Function
harmonica.isostatic_moho_airy computes the depth to crust-mantle
interface (the Moho) according to Airy isostasy. The function takes the depth
to the crystalline basement and optionally any layers on top of it. Each layer
is defined by its thickness and its density. In addition, one must assume
a value for the reference thickness of the continental crust in order to
convert the root/anti-root thickness into Moho depth. The function contains
common default values for the reference thickness and crust, mantle
[TurcotteSchubert2014].
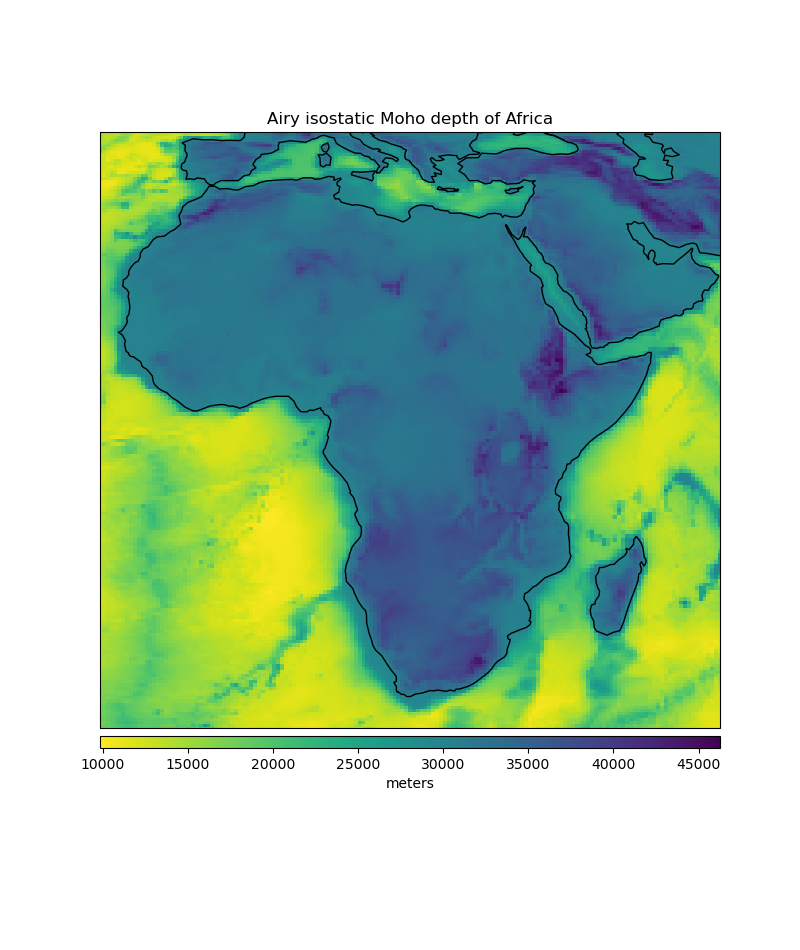
We’ll use our sample topography data
(harmonica.datasets.fetch_topography_earth) to calculate the Airy
isostatic Moho depth of Africa.
Out:
Topography/bathymetry grid:
<xarray.Dataset>
Dimensions: (latitude: 171, longitude: 161)
Coordinates:
* longitude (longitude) float64 -20.0 -19.5 -19.0 -18.5 ... 59.0 59.5 60.0
* latitude (latitude) float64 -40.0 -39.5 -39.0 -38.5 ... 44.0 44.5 45.0
Data variables:
topography (latitude, longitude) float64 -3.523e+03 -3.392e+03 ... 29.0
Attributes: (12/31)
generating_institute: gfz-potsdam
generating_date: 2018/12/13
product_type: topography
body: earth
modelname: etopo1-2250
max_used_degree: 1277
... ...
maxvalue: 5.6509528E+03 meter
minvalue: -8.4094822E+03 meter
signal_wrms: 2.4872117E+03 meter
grid_format: long_lat_value
attributes: longitude latitude topography
attributes_units: deg. deg. meter
Moho depth grid:
<xarray.DataArray 'moho_depth' (latitude: 171, longitude: 161)>
array([[17528.58, 17992.32, 18169.32, ..., 11793.78, 11712.36, 11499.96],
[17733.9 , 18148.08, 18679.08, ..., 11436.24, 11432.7 , 11372.52],
[17471.94, 17946.3 , 18604.74, ..., 11269.86, 11411.46, 11397.3 ],
...,
[15149.7 , 13783.26, 13397.4 , ..., 30229.6 , 30207.2 , 30218.4 ],
[15153.24, 14215.14, 13623.96, ..., 30184.8 , 30162.4 , 30162.4 ],
[15139.08, 14622.24, 13900.08, ..., 30207.2 , 30184.8 , 30162.4 ]])
Coordinates:
* longitude (longitude) float64 -20.0 -19.5 -19.0 -18.5 ... 59.0 59.5 60.0
* latitude (latitude) float64 -40.0 -39.5 -39.0 -38.5 ... 44.0 44.5 45.0
Attributes:
isostasy: Airy
density_crust: 2800.0
density_mantle: 3300.0
density_water: 1030
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
import numpy as np
import harmonica as hm
# Load the elevation model and cut out the portion of the data corresponding to
# Africa
data = hm.datasets.fetch_topography_earth()
region = (-20, 60, -40, 45)
data_africa = data.sel(latitude=slice(*region[2:]), longitude=slice(*region[:2]))
print("Topography/bathymetry grid:")
print(data_africa)
# Calculate the water thickness
oceans = np.array(data_africa.topography < 0)
water_thickness = data_africa.topography * oceans * -1
water_density = 1030
# Calculate the isostatic Moho depth using the default values for densities and
# reference Moho with water load. We neglect the effect of sediment here, so
# basement elevation refers to topography.
moho = hm.isostatic_moho_airy(
basement=data_africa.topography,
layers={"water": (water_thickness, water_density)},
)
print("\nMoho depth grid:")
print(moho)
# Draw the maps
plt.figure(figsize=(8, 9.5))
ax = plt.axes(projection=ccrs.LambertCylindrical(central_longitude=20))
pc = moho.plot.pcolormesh(
ax=ax, cmap="viridis_r", add_colorbar=False, transform=ccrs.PlateCarree()
)
plt.colorbar(pc, ax=ax, orientation="horizontal", pad=0.01, aspect=50, label="meters")
ax.coastlines()
ax.set_title("Airy isostatic Moho depth of Africa")
ax.set_extent(region, crs=ccrs.PlateCarree())
plt.show()
Total running time of the script: ( 0 minutes 0.240 seconds)
