Topography-free (Bouguer) Gravity Disturbances¶

The gravity disturbance is the observed gravity minus the normal gravity (boule.Ellipsoid.normal_gravity). The signal that is left is assumed to be due to the differences between the actual Earth and the reference ellipsoid. Big components in this signal are the effects of topographic masses outside of the ellipsoid and residual effects of the oceans (we removed ellipsoid crust where there was actually ocean water). These two components are relatively well known and can be removed from the gravity disturbance. The simplest way of calculating the effects of topography and oceans is through the Bouguer plate approximation.

We’ll use harmonica.bouguer_correction to calculate a topography-free gravity disturbance for Earth using our sample gravity and topography data. One thing to note is that the ETOPO1 topography is referenced to the geoid, not the ellipsoid. Since we want to remove the masses between the surface of the Earth and ellipsoid, we need to add the geoid height to the topography before Bouguer correction.

Topography-free (Bouguer) gravity of disturbance of the Earth

Out:

<xarray.Dataset>
Dimensions:          (latitude: 361, longitude: 721)
Coordinates:
  * longitude        (longitude) float64 -180.0 -179.5 -179.0 ... 179.5 180.0
  * latitude         (latitude) float64 -90.0 -89.5 -89.0 ... 89.0 89.5 90.0
Data variables:
    gravity          (latitude, longitude) float64 9.801e+05 ... 9.802e+05
    height_over_ell  (latitude, longitude) float64 1e+04 1e+04 ... 1e+04 1e+04
    geoid            (latitude, longitude) float64 -29.5 -29.5 ... 15.37 15.37
    topography       (latitude, longitude) float64 2.762e+03 ... -4.179e+03
Attributes: (12/35)
    generating_institute:  gfz-potsdam
    generating_date:       2018/11/07
    product_type:          gravity_field
    body:                  earth
    modelname:             EIGEN-6C4
    max_used_degree:       1277
    ...                    ...
    maxvalue:              9.8018358E+05 mgal
    minvalue:              9.7476403E+05 mgal
    signal_wrms:           1.5467865E+03 mgal
    grid_format:           long_lat_value
    attributes:            longitude latitude gravity_ell
    attributes_units:      deg. deg. mgal

import boule as bl
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
import xarray as xr

import harmonica as hm

# Load the global gravity, topography, and geoid grids
data = xr.merge(
    [
        hm.datasets.fetch_gravity_earth(),
        hm.datasets.fetch_geoid_earth(),
        hm.datasets.fetch_topography_earth(),
    ]
)
print(data)

# Calculate normal gravity and the disturbance
ellipsoid = bl.WGS84
gamma = ellipsoid.normal_gravity(data.latitude, data.height_over_ell)
disturbance = data.gravity - gamma

# Reference the topography to the ellipsoid
topography_ell = data.topography + data.geoid

# Calculate the Bouguer planar correction and the topography-free disturbance.
# Use the default densities for the crust and ocean water.
bouguer = hm.bouguer_correction(topography_ell)
disturbance_topofree = disturbance - bouguer

# Make a plot of data using Cartopy
plt.figure(figsize=(10, 10))
ax = plt.axes(projection=ccrs.Orthographic(central_longitude=-60))
pc = disturbance_topofree.plot.pcolormesh(
    ax=ax, transform=ccrs.PlateCarree(), add_colorbar=False
)
plt.colorbar(
    pc, label="mGal", orientation="horizontal", aspect=50, pad=0.01, shrink=0.5
)
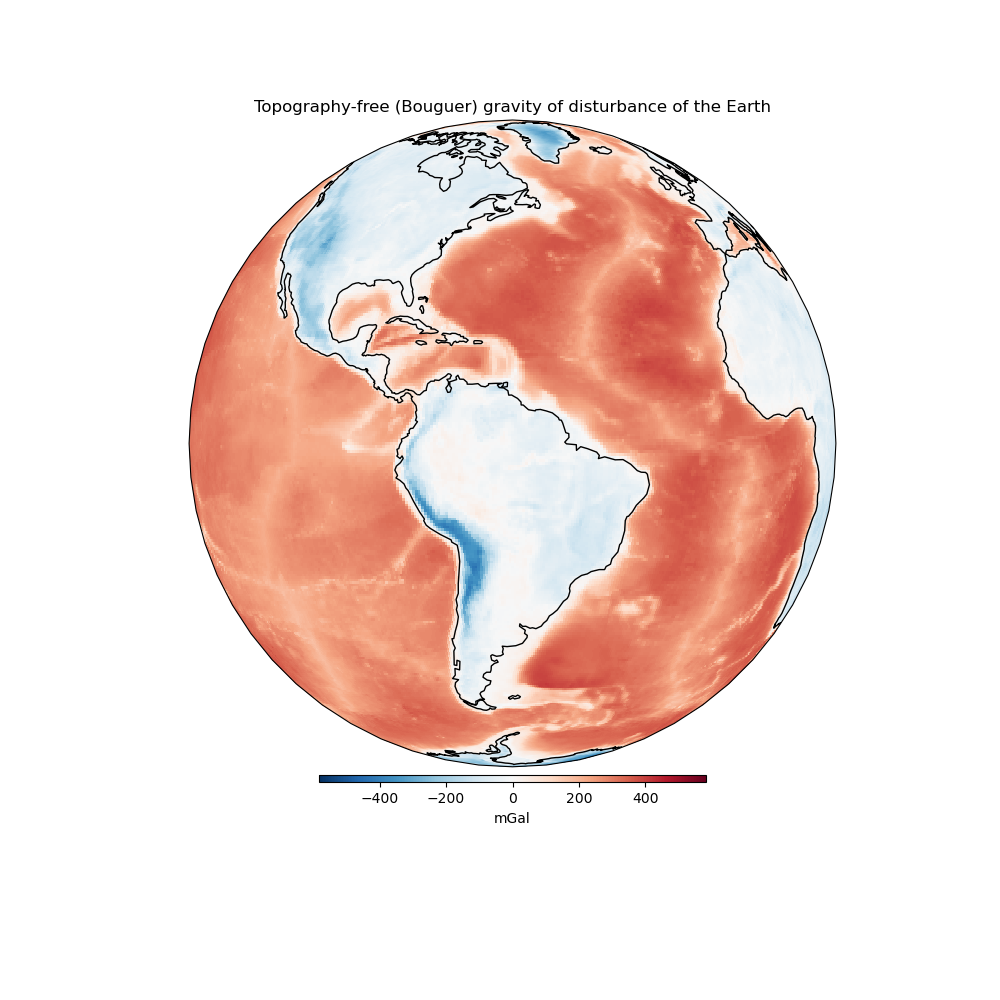
ax.set_title("Topography-free (Bouguer) gravity of disturbance of the Earth")
ax.coastlines()
plt.show()

Total running time of the script: ( 0 minutes 2.309 seconds)

Gallery generated by Sphinx-Gallery

Harmonica v0.5.0

Topography-free (Bouguer) Gravity Disturbances

Topography-free (Bouguer) Gravity Disturbances¶