Block-averaged equivalent sources

Block-averaged equivalent sources

When we introduced the Equivalent Sources we saw that by default the harmonica.EquivalentSources class locates one point source beneath each data point during the fitting process, following [Cooper2000].

Alternatively, we can use another strategy: the block-averaged sources, introduced in [Soler2021]. This method divides the survey region (defined by the data) into square blocks of equal size, computes the median coordinates of the data points that fall inside each block and locates one source beneath every averaged position. This way, we define one equivalent source per block, with the exception of empty blocks that won’t get any source.

This method has two main benefits:

  • It lowers the amount of sources involved in the interpolation, therefore it reduces the computer memory requirements and the computation time of the fitting and prediction processes.

  • It might avoid to produce aliasing on the output grids, specially for surveys with oversampling along a particular direction, like airborne ones.

We can make use of the block-averaged sources within the harmonica.EquivalentSources class by passing a value to the block_size parameter, which controls the size of the blocks.

Lets load some total-field magnetic data over Great Britain:

import ensaio
import pandas as pd

fname = ensaio.fetch_britain_magnetic(version=1)
data = pd.read_csv(fname)
data
line_and_segment year longitude latitude height_m total_field_anomaly_nt
0 FL1-1 1955 -1.74162 53.48164 792 62
1 FL1-1 1955 -1.70122 53.48352 663 56
2 FL1-1 1955 -1.08051 53.47677 315 30
3 FL1-1 1955 -1.07471 53.47672 315 31
4 FL1-1 1955 -1.01763 53.47586 321 44
... ... ... ... ... ... ...
541503 FL-3(TL10-24)-1 1965 -4.68843 58.26786 1031 64
541504 FL-3(TL10-24)-1 1965 -4.68650 58.26786 1045 74
541505 FL-3(TL10-24)-1 1965 -4.68535 58.26790 1035 94
541506 FL-3(TL10-24)-1 1965 -4.68419 58.26787 1024 114
541507 FL-3(TL10-24)-1 1965 -4.68274 58.26790 1011 120

541508 rows × 6 columns

In order to speed-up calculations we are going to slice a smaller portion of the data:

import verde as vd

region = (-5.5, -4.7, 57.8, 58.5)
inside = vd.inside((data.longitude, data.latitude), region)
data = data[inside]
data
line_and_segment year longitude latitude height_m total_field_anomaly_nt
383858 FL-47-2 1964 -5.38345 57.95592 305 112
383859 FL-47-2 1964 -5.38180 57.95614 305 120
383860 FL-47-2 1964 -5.38011 57.95633 305 150
383861 FL-47-2 1964 -5.37851 57.95658 305 170
383862 FL-47-2 1964 -5.37650 57.95693 305 220
... ... ... ... ... ... ...
538970 FL-16(TL24-36)-6 1965 -4.70304 58.49978 319 162
541490 FL-11-5 1965 -4.88674 58.40691 1056 245
541491 FL-11-5 1965 -4.88377 58.40689 1069 250
541492 FL-11-5 1965 -4.88202 58.40724 1055 245
541493 FL-11-5 1965 -4.88047 58.40728 1041 234

7054 rows × 6 columns

And project the geographic coordiantes to plain Cartesian ones:

import pyproj

projection = pyproj.Proj(proj="merc", lat_ts=data.latitude.mean())
easting, northing = projection(data.longitude.values, data.latitude.values)
coordinates = (easting, northing, data.height_m)

import matplotlib.pyplot as plt

maxabs = vd.maxabs(data.total_field_anomaly_nt)

plt.scatter(
    easting,
    northing,
    c=data.total_field_anomaly_nt,
    cmap="seismic",
    vmin=-maxabs,
    vmax=maxabs,
)
plt.colorbar(aspect=40, pad=0.01, label="nT")
plt.gca().set_aspect("equal")
plt.gcf().set_size_inches(12, 9)
plt.title("Observed total-field magnetic anomaly")
plt.xlabel("easting [m]")
plt.ylabel("northing [m]")
plt.show()
../../_images/block-averaged-eqs_3_0.png

Most airborne surveys like this one present an anysotropic distribution of the data: there are more observation points along the flight lines that goes west to east than the ones going south to north. Placing a single source beneath each observation point generates an anysotropic distribution of the equivalent sources, which might lead to aliases on the generated outputs.

Instead, we can use the block-averaged equivalent sources by creating a harmonica.EquivalentSources instance passing the size of the blocks through the block_size parameter.

import harmonica as hm

eqs = hm.EquivalentSources(
    depth=1000, damping=1, block_size=500, depth_type="constant"
)

These sources were set at a constant depth of 1km bellow the zeroth height and with a damping equal to 1. See how you can choose values for these parameters in Estimating damping and depth parameters.

Note

The depth of the sources can be set analogously to the regular equivalent sources: we can use a constant depth (every source is located at the same depth) or a relative depth (where each source is located at a constant shift beneath the median location obtained during the block-averaging process). The depth of the sources and which strategy to use can be set up through the depth and the depth_type parameters, respectively.

Important

We recommend using a block_size not larger than the desired resolution of the interpolation grid.

Now we can fit the equivalent sources against the magnetic data. During this step the point sources are created through the block averaging process.

eqs.fit(coordinates, data.total_field_anomaly_nt)

EquivalentSources(block_size=500, damping=1, depth=1000, depth_type='constant')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Tip

We can obtain the coordinates of the created sources through the points_ attribute. Lets see how many sources it created:

eqs.points_[0].size

3368

We have less sources than observation points indeed.

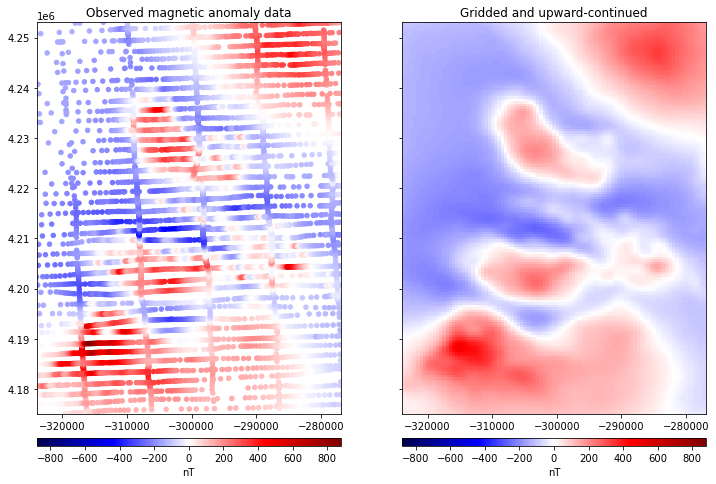
We can finally grid the magnetic data using the block-averaged equivalent sources. We will generate a regular grid with a resolution of 500 m and at 1500 m height. Since the maximum height of the observation points is around 1000 m we are efectivelly upward continuing the data.

grid_coords = vd.grid_coordinates(
    region=vd.get_region(coordinates),
    spacing=500,
    extra_coords=1500,
)
grid = eqs.grid(grid_coords, data_names=["magnetic_anomaly"])
grid

<xarray.Dataset>
Dimensions:           (northing: 157, easting: 95)
Coordinates:
  * easting           (easting) float64 -3.24e+05 -3.235e+05 ... -2.769e+05
  * northing          (northing) float64 4.175e+06 4.176e+06 ... 4.253e+06
    upward            (northing, easting) float64 1.5e+03 1.5e+03 ... 1.5e+03
Data variables:
    magnetic_anomaly  (northing, easting) float64 28.68 28.71 ... 167.5 157.7
Attributes:
    metadata:  Generated by EquivalentSources(block_size=500, damping=1, dept...
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 9), sharey=True)

# Get the maximum absolute value between the original and gridded data so we
# can use the same color scale for both plots and have 0 centered at the white
# color.
maxabs = vd.maxabs(data.total_field_anomaly_nt, grid.magnetic_anomaly.values)

ax1.set_title("Observed magnetic anomaly data")
tmp = ax1.scatter(
    easting,
    northing,
    c=data.total_field_anomaly_nt,
    s=20,
    vmin=-maxabs,
    vmax=maxabs,
    cmap="seismic",
)
plt.colorbar(tmp, ax=ax1, label="nT", pad=0.05, aspect=40, orientation="horizontal")
ax1.set_xlim(easting.min(), easting.max())
ax1.set_ylim(northing.min(), northing.max())

ax2.set_title("Gridded and upward-continued")
tmp = grid.magnetic_anomaly.plot.pcolormesh(
    ax=ax2,
    add_colorbar=False,
    add_labels=False,
    vmin=-maxabs,
    vmax=maxabs,
    cmap="seismic",
)
plt.colorbar(tmp, ax=ax2, label="nT", pad=0.05, aspect=40, orientation="horizontal")
ax2.set_xlim(easting.min(), easting.max())
ax2.set_ylim(northing.min(), northing.max())

plt.show()
../../_images/block-averaged-eqs_8_0.png

previous

Estimating damping and depth parameters

next

Gradient-boosted equivalent sources