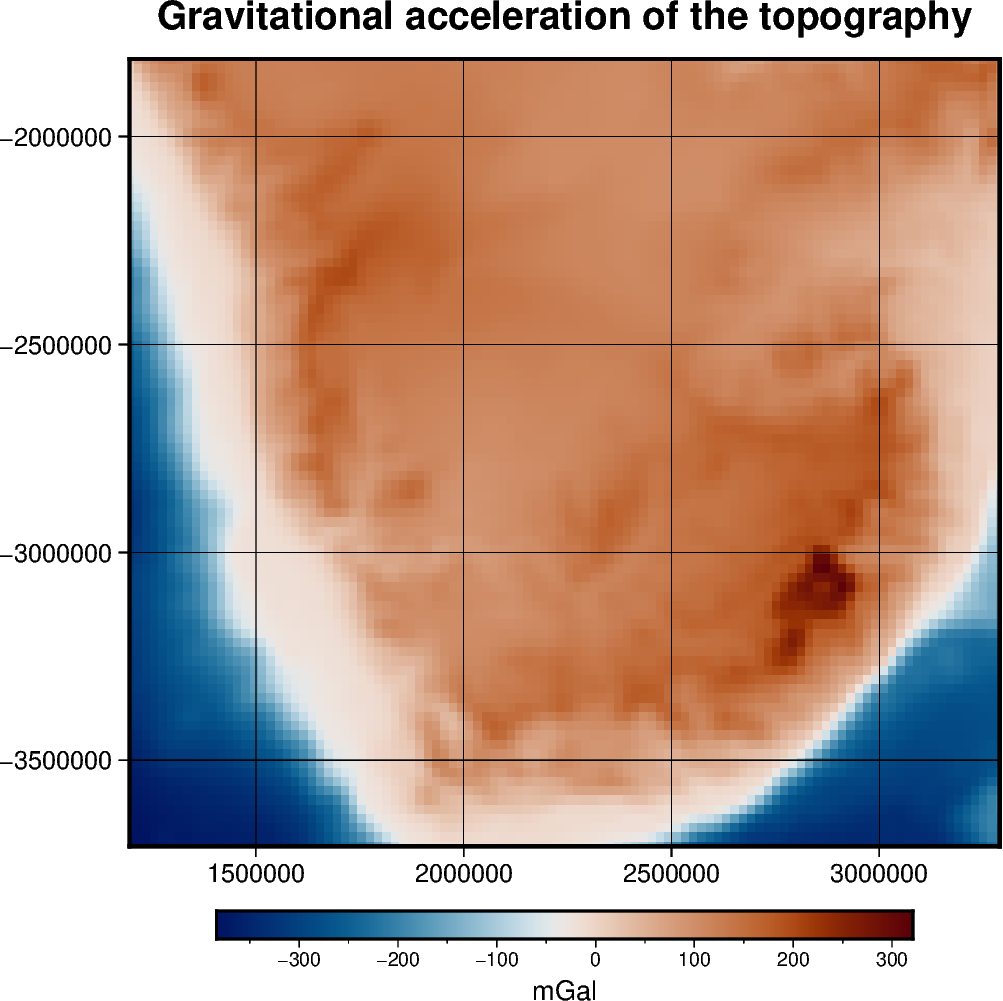
Gravitational effect of topography

One possible application of the harmonica.prism_layer function is to create a model of the terrain and compute its gravity effect. Here we will use a regular grid of topographic and bathymetric heights for South Africa to create a prisms layer that model the terrain with a density of 2670 kg/m^3 and the ocean with a density contrast of -1900 kg/m^3 obtained as the difference between the density of water (1000 kg/m^3) and the normal density of upper crust (2900 kg/m^3). Then we will use harmonica.prism_gravity to compute the gravity effect of the model on a regular grid of observation points.

/home/runner/miniconda3/envs/test/lib/python3.12/site-packages/pygmt/clib/session.py:1498: RuntimeWarning: Grid may have irregular spacing in the 'northing' dimension, but GMT only supports regular spacing. Calculated regular spacing 22283.15174176384 is assumed in the 'northing' dimension.
  matrix, region, inc = dataarray_to_matrix(grid)

import ensaio
import pygmt
import pyproj
import verde as vd
import xarray as xr

import harmonica as hm

# Read Earth's topography grid
fname = ensaio.fetch_earth_topography(version=1)
topography = xr.load_dataset(fname)

# Crop the topography limited to South Africa
region = (12, 33, -35, -18)
region_padded = vd.pad_region(region, pad=5)  # pad the original region
topography = topography.sel(
    longitude=slice(*region_padded[:2]),
    latitude=slice(*region_padded[2:]),
)

# Project the grid
projection = pyproj.Proj(proj="merc", lat_ts=topography.latitude.values.mean())
south_africa_topo = vd.project_grid(topography.topography, projection=projection)

# Create a 2d array with the density of the prisms Points above the geoid will
# have a density of 2670 kg/m^3 Points below the geoid will have a density
# contrast equal to the difference between the density of the ocean and the
# density of the upper crust: # 1000 kg/m^3 - 2900 kg/m^3
density = south_africa_topo.copy()  # copy topography to a new xr.DataArray
density.values[:] = 2670.0  # replace every value for the density of the topography
# Change density values of ocean points
density = density.where(south_africa_topo >= 0, 1000 - 2900)

# Create layer of prisms
prisms = hm.prism_layer(
    (south_africa_topo.easting, south_africa_topo.northing),
    surface=south_africa_topo,
    reference=0,
    properties={"density": density},
)

# Compute gravity field on a regular grid located at 4000m above the ellipsoid
coordinates = vd.grid_coordinates(region=region, spacing=0.2, extra_coords=4000)
easting, northing = projection(*coordinates[:2])
coordinates_projected = (easting, northing, coordinates[-1])
prisms_gravity = prisms.prism_layer.gravity(coordinates_projected, field="g_z")

# merge into a dataset
grid = vd.make_xarray_grid(
    coordinates_projected,
    prisms_gravity,
    data_names="gravity",
    extra_coords_names="extra",
)

# Set figure properties
xy_region = vd.get_region((easting, northing))
w, e, s, n = xy_region
fig_height = 10
fig_width = fig_height * (e - w) / (n - s)
fig_ratio = (n - s) / (fig_height / 100)
fig_proj = f"x1:{fig_ratio}"

# Make a plot of the computed gravity
fig = pygmt.Figure()

title = "Gravitational acceleration of the topography"

with pygmt.config(FONT_TITLE="14p"):
    fig.grdimage(
        region=xy_region,
        projection=fig_proj,
        grid=grid.gravity,
        frame=["ag", f"+t{title}"],
        cmap="vik",
    )

fig.colorbar(cmap=True, frame=["a100f50", "x+lmGal"])

fig.show()