Note
Go to the end to download the full example code
Gradient-boosted equivalent sources#
When trying to grid a very large dataset, the regular
harmonica.EquivalentSources might not be the best option: they will
require a lot of memory for storing the Jacobian matrices involved in the
fitting process of the source coefficients. Instead, we can make use of the
gradient-boosted equivalent sources, introduced in [Soler2021] and available
in Harmonica through the harmonica.EquivalentSourcesGB class. The
gradient-boosted equivalent sources divide the survey region in overlapping
windows of equal size and fit the source coefficients iteratively, considering
the sources and data points that fall under each window at a time. The order in
which the windows are visited is randomized to improve convergence of the
algorithm.
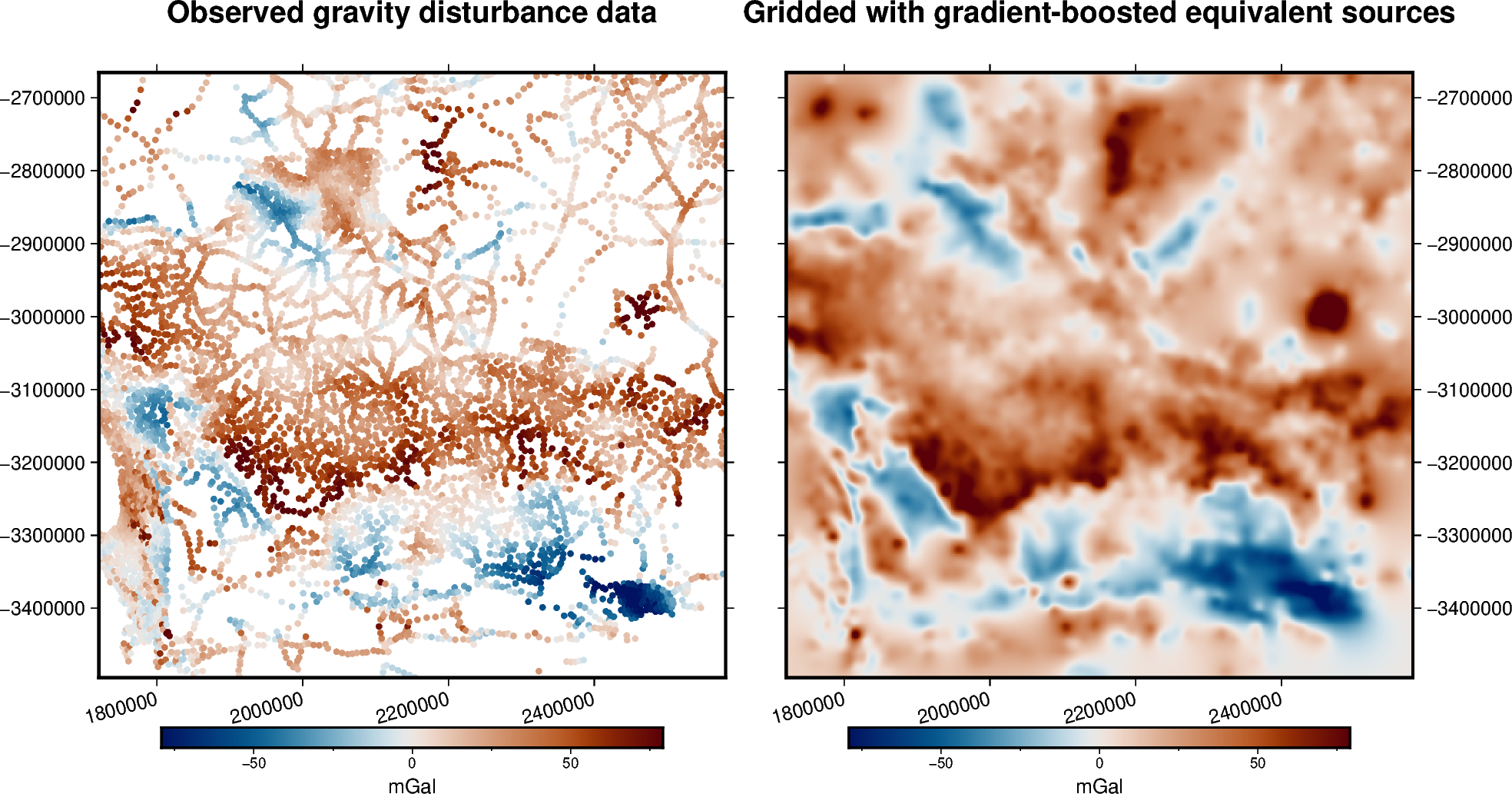
Here we will produce a grid out of a portion of the ground gravity survey from
South Africa (see harmonica.datasets.fetch_south_africa_gravity) using
the gradient-boosted equivalent sources. This particlar dataset is not very
large, in fact we could use the harmonica.EquivalentSources instead.
But we will use the harmonica.EquivalentSourcesGB for illustrating how
to use them on a small example.
Number of data points: 6342
Mean height of observations: 868.9293913591926
Required memory for storing the largest Jacobian: 672792 bytes
Number of sources: 6231
R² score: 0.980707030192003
<xarray.Dataset> Size: 3MB
Dimensions: (northing: 416, easting: 431)
Coordinates:
* easting (easting) float64 3kB 1.72e+06 1.722e+06 ... 2.58e+06
* northing (northing) float64 3kB -3.495e+06 ... -2.665e+06
upward (northing, easting) float64 1MB 1e+03 1e+03 ... 1e+03
Data variables:
gravity_disturbance (northing, easting) float64 1MB 7.169 7.235 ... 17.69
Attributes:
metadata: Generated by EquivalentSourcesGB(block_size=2000.0, damping=10...
import boule as bl
import ensaio
import pandas as pd
import pygmt
import pyproj
import verde as vd
import harmonica as hm
# Fetch the sample gravity data from South Africa
fname = ensaio.fetch_southern_africa_gravity(version=1)
data = pd.read_csv(fname)
# Slice a smaller portion of the survey data to speed-up calculations for this
# example
region = [18, 27, -34.5, -27]
inside = vd.inside((data.longitude, data.latitude), region)
data = data[inside]
print("Number of data points:", data.shape[0])
print("Mean height of observations:", data.height_sea_level_m.mean())
# Since this is a small area, we'll project our data and use Cartesian
# coordinates
projection = pyproj.Proj(proj="merc", lat_ts=data.latitude.mean())
easting, northing = projection(data.longitude.values, data.latitude.values)
coordinates = (easting, northing, data.height_sea_level_m)
xy_region = vd.get_region((easting, northing))
# Compute the gravity disturbance
ellipsoid = bl.WGS84
data["gravity_disturbance"] = data.gravity_mgal - ellipsoid.normal_gravity(
data.latitude, data.height_sea_level_m
)
# Create the equivalent sources
# We'll use the block-averaged sources with a block size of 2km and windows of
# 100km x 100km, a damping of 10 and set the sources at a relative depth of
# 9km. By specifying the random_state, we ensure to get the same solution on
# every run.
window_size = 100e3
block_size = 2e3
eqs_gb = hm.EquivalentSourcesGB(
depth=9e3,
damping=10,
window_size=window_size,
block_size=block_size,
random_state=42,
)
# Let's estimate the memory required to store the largest Jacobian when using
# these values for the window_size and the block_size.
jacobian_req_memory = eqs_gb.estimate_required_memory(coordinates)
print(f"Required memory for storing the largest Jacobian: {jacobian_req_memory} bytes")
# Fit the sources coefficients to the observed gravity disturbance.
eqs_gb.fit(coordinates, data.gravity_disturbance)
print("Number of sources:", eqs_gb.points_[0].size)
# Evaluate the data fit by calculating an R² score against the observed data.
# This is a measure of how well the sources fit the data, NOT how good the
# interpolation will be.
print("R² score:", eqs_gb.score(coordinates, data.gravity_disturbance))
# Interpolate data on a regular grid with 2 km spacing. The interpolation
# requires the height of the grid points (upward coordinate). By passing in
# 1000 m, we're effectively upward-continuing the data.
grid_coords = vd.grid_coordinates(region=xy_region, spacing=2e3, extra_coords=1000)
grid = eqs_gb.grid(coordinates=grid_coords, data_names="gravity_disturbance")
print(grid)
# Set figure properties
w, e, s, n = xy_region
fig_height = 10
fig_width = fig_height * (e - w) / (n - s)
fig_ratio = (n - s) / (fig_height / 100)
fig_proj = f"x1:{fig_ratio}"
# Plot the original gravity disturbance and the gridded and upward-continued
# version
fig = pygmt.Figure()
title = "Observed gravity disturbance data"
# Make colormap of data
pygmt.makecpt(
cmap="vik",
series=(
-data.gravity_disturbance.quantile(0.99),
data.gravity_disturbance.quantile(0.99),
),
background=True,
)
with pygmt.config(FONT_TITLE="14p"):
fig.plot(
projection=fig_proj,
region=xy_region,
frame=[f"WSne+t{title}", "xa200000+a15", "ya100000"],
x=easting,
y=northing,
fill=data.gravity_disturbance,
style="c0.1c",
cmap=True,
)
fig.colorbar(cmap=True, frame=["a50f25", "x+lmGal"])
fig.shift_origin(xshift=fig_width + 1)
title = "Gridded with gradient-boosted equivalent sources"
with pygmt.config(FONT_TITLE="14p"):
fig.grdimage(
frame=[f"ESnw+t{title}", "xa200000+a15", "ya100000"],
grid=grid.gravity_disturbance,
cmap=True,
)
fig.colorbar(cmap=True, frame=["a50f25", "x+lmGal"])
fig.show()
Total running time of the script: (0 minutes 5.637 seconds)