Gravitational effect of topography

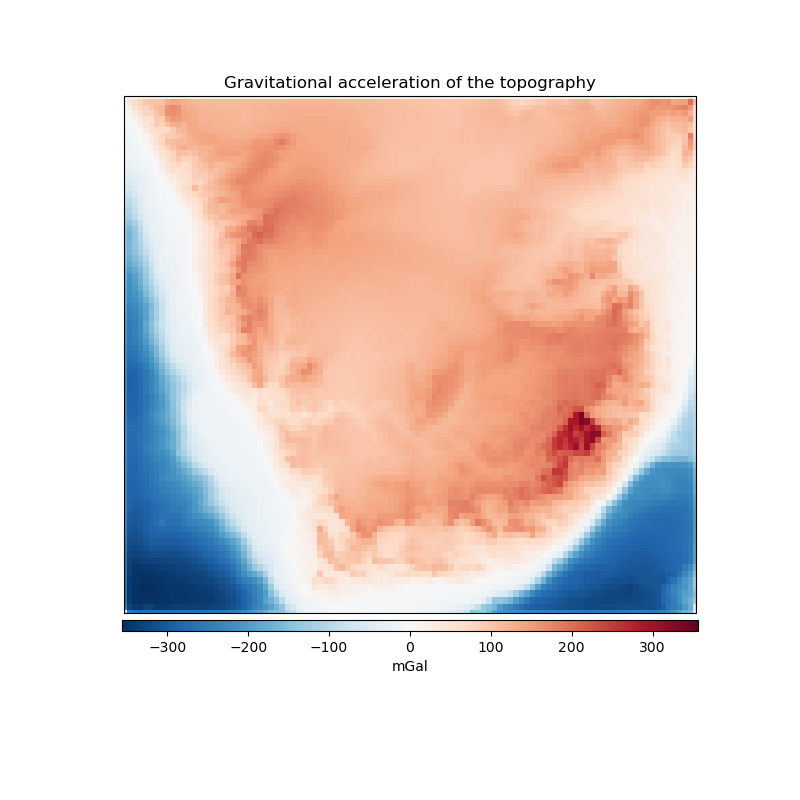
One possible application of the harmonica.prisms_layer function is to create a model of the terrain and compute its gravity effect. Here we will use a regular grid of topographic and bathymetric heights for South Africa to create a prisms layer that model the terrain with a density of 2670 kg/m^3 and the ocean with a density contrast of -1900 kg/m^3 obtained as the difference between the density of water (1000 kg/m^3) and the normal density of upper crust (2900 kg/m^3). Then we will use harmonica.prism_gravity to compute the gravity effect of the model on a regular grid of observation points.

import pyproj
import numpy as np
import verde as vd
import harmonica as hm
import matplotlib.pyplot as plt
import cartopy.crs as ccrs


# Read South Africa topography
south_africa_topo = hm.datasets.fetch_south_africa_topography()

# Project the grid
projection = pyproj.Proj(proj="merc", lat_ts=south_africa_topo.latitude.values.mean())
south_africa_topo = vd.project_grid(south_africa_topo.topography, projection=projection)

# Create a 2d array with the density of the prisms Points above the geoid will
# have a density of 2670 kg/m^3 Points below the geoid will have a density
# contrast equal to the difference between the density of the ocean and the
# density of the upper crust: # 1000 kg/m^3 - 2900 kg/m^3
density = south_africa_topo.copy()  # copy topography to a new xr.DataArray
density.values[:] = 2670.0  # replace every value for the density of the topography
# Change density values of ocean points
density = density.where(south_africa_topo >= 0, 1000 - 2900)

# Create layer of prisms
prisms = hm.prisms_layer(
    (south_africa_topo.easting, south_africa_topo.northing),
    surface=south_africa_topo.values,
    reference=0,
    properties={"density": density},
)

# Compute gravity field on a regular grid located at 4000m above the ellipsoid
coordinates = vd.grid_coordinates(
    region=(12, 33, -35, -18), spacing=0.2, extra_coords=4000
)
easting, northing = projection(*coordinates[:2])
coordinates_projected = (easting, northing, coordinates[-1])
prisms_gravity = prisms.prisms_layer.gravity(coordinates_projected, field="g_z")

# Make a plot of the computed gravity
plt.figure(figsize=(8, 8))
ax = plt.axes(projection=ccrs.Mercator())
maxabs = vd.maxabs(prisms_gravity)
tmp = ax.pcolormesh(
    *coordinates[:2],
    prisms_gravity,
    vmin=-maxabs,
    vmax=maxabs,
    cmap="RdBu_r",
    transform=ccrs.PlateCarree()
)
ax.set_extent(vd.get_region(coordinates), crs=ccrs.PlateCarree())
plt.title("Gravitational acceleration of the topography")
plt.colorbar(
    tmp, label="mGal", orientation="horizontal", shrink=0.93, pad=0.01, aspect=50
)
plt.show()